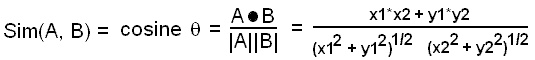Singular_Value_Decomposition_Tutorial.pdf
Singular_Value_Decomposition_Tutorial.pdf
LSA(Latent Semantic Analysis)를 구현하기 위해서 알아야 할 것들이 몇 가지 있다.
우선 SVD( Singular Value Decompositon )을 알아야 한다.
SVD에 대한 설명 아래 블로그에 가서 보면 도움이 될것이다.
SVD 설명 : http://blog.daum.net/hazzling/15807155
SVD 라이브러리 : http://tedlab.mit.edu/~dr/SVDLIBC/
svd 공부하기전에 알아야 할 것들
- vector length = [4, 11, 8, 10] |v| = sqrt(4^2 + 11^2 + 8^2 + 10^2) = p301 = 17.35
- Orthogonality = [2, 1,-2, 4] and [3,-6, 4, 2] [2, 1,-2, 4] * [3,-6, 4, 2] = 2(3) + 1(-6) - 2(4) + 4(2) = 0
- Normal vector = unit vector = vector length가 1인 vector
- transpose = 행렬의 행과 열은 바꾸는 것
- Orthogonal Matrix = A^T와 A는 orthogonal하다
- digonal matrix = 대각선에만 값이 있는 행렬
- Determinant =
n = 2
n > 2
그리고 또한가지 일반적으로 백터의 유사도를 계산하기 위해서 사용하는 코사인 유사도( cosine similarity )는
대용량에서 문서와 문서와의 관계 텀과 텀의 관계에서 어떤 보이지 않는 정보를 추출할때 사용하는 방법론이 LSA이다.
간단하게 작은 샘플을 가지고 어떤 능력이 있는지 살펴보자
우선
6개의 문서가 있다.
문서 1: cosmonaut, moon, car
문서 2 : astronaut, moon
문서 3 : cosmonaut
문서 4 : car, truck
문서 5 : car
문서 6 : truck
이렇게 6개의 문서가 있는데
사람이 보고 유사한 문서를 찾으면
term을 기준으로 같은 텀이 들어간 4,5번 문서가 유사하고, 1,2번 문서가 유사하다고 말할것이다.
그런데 LSA는 이것말고 이 안에 숨겨진 다른 정보를 보여준다.
우선
위 6개의 문서를 행렬로 표현하면
A =
| d1 | d2 | d3 | d4 | d5 | d6 | |
| cosmonaut | 1 | 0 | 1 | 0 | 0 | 0 |
| astronaut | 0 | 1 | 0 | 0 | 0 | 0 |
| moon | 1 | 1 | 0 | 0 | 0 | 0 |
| car | 1 | 0 | 0 | 1 | 1 | 0 |
| truck | 0 | 0 | 0 | 1 | 0 | 1 |
A라는 행렬에 숨겨진 정보를 찾기 위해서 SVD라는 것을 사용하는데
간단하게 설명하면 원본 행렬 A를 3개의 행렬로 분리하는 것이다.
공식으로 쓰면 A = USV 라고 쓰고
아래 보이는 테이블이 첫부분에 소개한 svdlibc로 얻은 값이다.
U=
| dim1 | dim2 | dim3 | dim4 | dim5 | |
| cosmonaut | -0.44 | -0.3 | 0.57 | 0.58 | 0.25 |
| astronaut | -0.13 | -0.33 | -0.59 | 0 | 0.73 |
| moon | -0.48 | -0.51 | -0.37 | 0 | -0.61 |
| car | -0.7 | 0.35 | 0.15 | -0.58 | 0.16 |
| truck | -0.26 | 0.65 | -0.41 | 0.58 | -0.09 |
S=
| 2.16 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.00 | 1.59 | 0.00 | 0.00 | 0.00 |
| 0.00 | 0.00 | 1.28 | 0.00 | 0.00 |
| 0.00 | 0.00 | 0.00 | 1.00 | 0.00 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.39 |
V =
| d1 | d2 | d3 | d4 | d5 | d6 | |
| dimension1 | -0.75 | -0.28 | -0.2 | -0.45 | -0.33 | -0.12 |
| dimension2 | -0.29 | -0.53 | -0.19 | 0.63 | 0.22 | 0.41 |
| dimension3 | 0.28 | -0.75 | 0.45 | -0.2 | 0.12 | -0.33 |
| dimension4 | 0 | 0 | 0.58 | 0 | -0.58 | 0.58 |
| dimension5 | -0.53 | 0.29 | 0.63 | 0.19 | 0.41 | -0.22 |
이렇게 계산된 값중에 행렬 S에서 2*2만을 위하여
V와 곱한다.
B=S*V
그러면 아래와 같은 행렬이 만들어진다.
| d1 | d2 | d3 | d4 | d5 | d6 | |
| dimension1 | -1.62 | -0.60 | -0.40 | -0.97 | -0.71 | -0.26 |
| dimension2 | -0.46 | -0.84 | -0.30 | 1.00 | 0.35 | 0.65 |
이들 사이의 cosine 유사도를 계산하면
DOC1 DOC2 DOC3 DOC4 DOC5 DOC6
DOC1 1 0 0 0 0 0
DOC2 0.781837 1 0 0 0 0
DOC3 0.950136 0.937276 1 0 0 0
DOC4 0.474432 -0.177918 0.176269 1 0 0
DOC5 0.740118 0.159375 0.493512 0.943112 1 0
DOC6 0.110596 -0.53319 -0.204841 0.927362 0.750205 1
위에 언급한 svdlibc 라이브러리고 위의 예제를 테스트 해본 결과 화면( cosine similarity를 사용 )
처음 데이터를 보면 d2,d3에는 하나의 공통 단어도 존재하지 않는다.
따라서 처음 데이터를 가지고 유사도를 계산한다면 0에 가까운 값이 나올 것이다.
그런데 SVD후에 유사도를 보면 유사도가 0.93으로 나온다.
문서 2에는 cosmonaut라는(러시아 우주비행사)가 있고 문서 3에는 astronaut(우주비행사)라는 의미적으로 유사한 단어가 포함되어 있음을 겉으로 드러낸 결과라고 할수 있다.
continue ---
'언어처리' 카테고리의 다른 글
| 조건부 확률 (1) | 2008.07.25 |
|---|---|
| Maximum Likelihood Estimation (0) | 2008.07.23 |
| Latent Semantic Analysis 2 (1) | 2008.05.13 |
| 띄어쓰기의 어려움 bigram 2-1 (1) | 2008.02.03 |
| Aho-Corasick 구현 (0) | 2007.11.01 |